进制

进位制又称进制，是一种记数方式，亦称位置记法（positional notation）、数字命位法、定位记法、进位记数法、位值记数法（place-value notation）、位置数值系统（positional numeral system）；利用这种“记数法”，可以使用有限种“数字符号”来表示所有的数值。

通常会在数字后加字母缩写后缀以区分不同进制，常用标识如下：

B: binary, 二进制, (0, 1)

O: octal, 八进制, (0, 1, 2, 3, 4, 5, 6, 7)

D: decimal, 十进制, (0, 1, 2, 3, 4, 5, 6, 7, 8, 9)

H: hex, 十六进制, (0-9, A, B, C, D, E)

进制间的转换

二、八、十六进制 到 十进制

二进制到十进制

101011B = 43D

步骤：

$1\times2^0 + 1\times2^1 + 0\times2^2 + 1\times2^3 + 0\times2^4 + 1\times2^5 = 43$

八进制到十进制

53O = 43D

步骤：

$3\times8^0 + 5\times8^1 = 43$

十六进制到十进制

2BH = 43D

步骤：

$11(B)\times16^0 + 2\times16^1 = 43$

十进制 到 二、八、十六进制

十进制到二进制

43D = 101011B

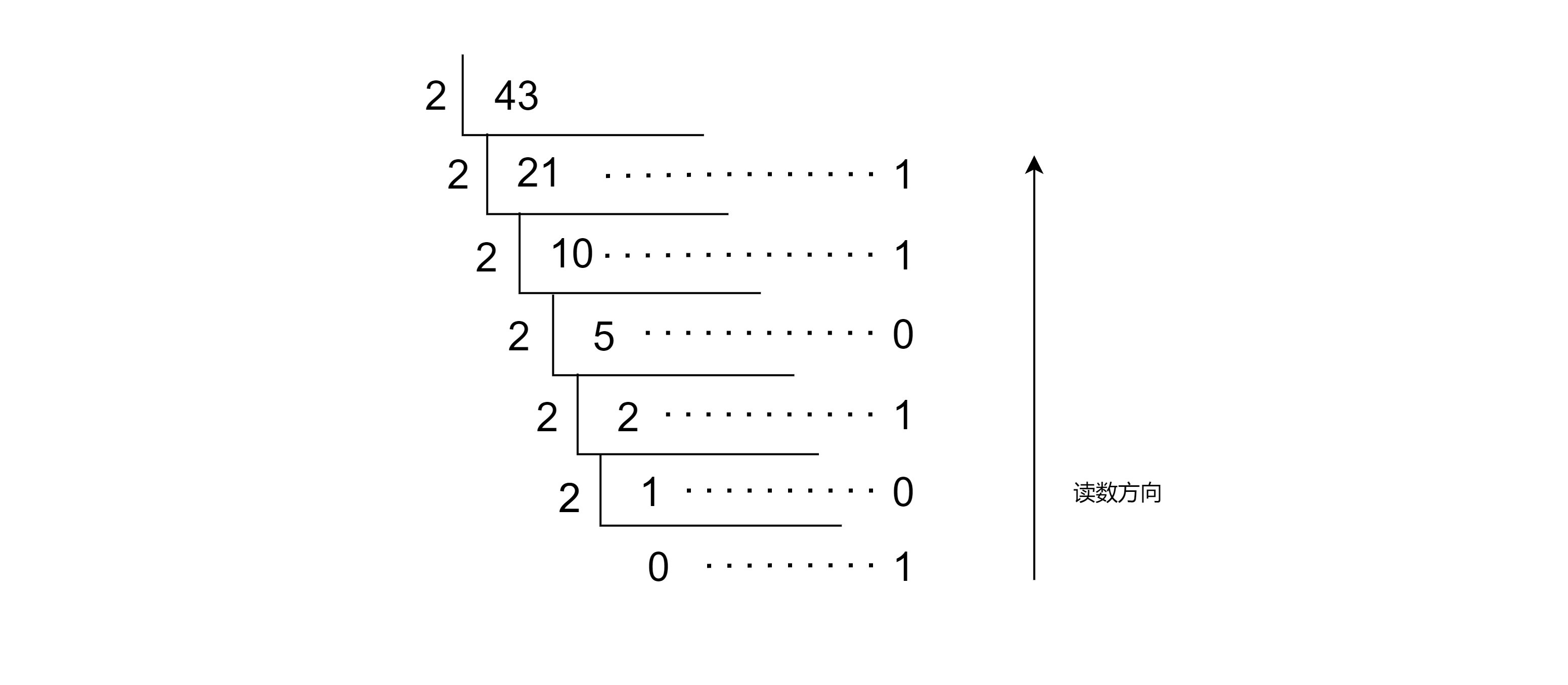
十进制到八进制

796D = 1434O

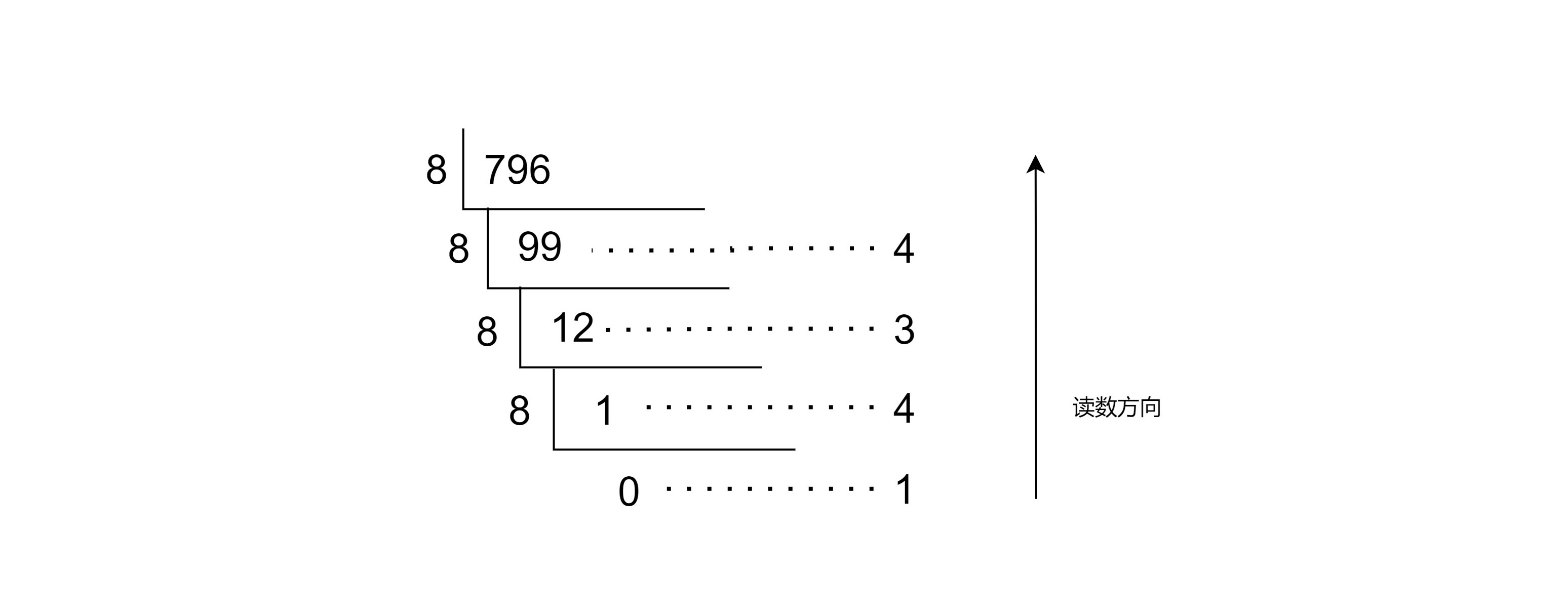
十进制到十六进制

796D = 31CH

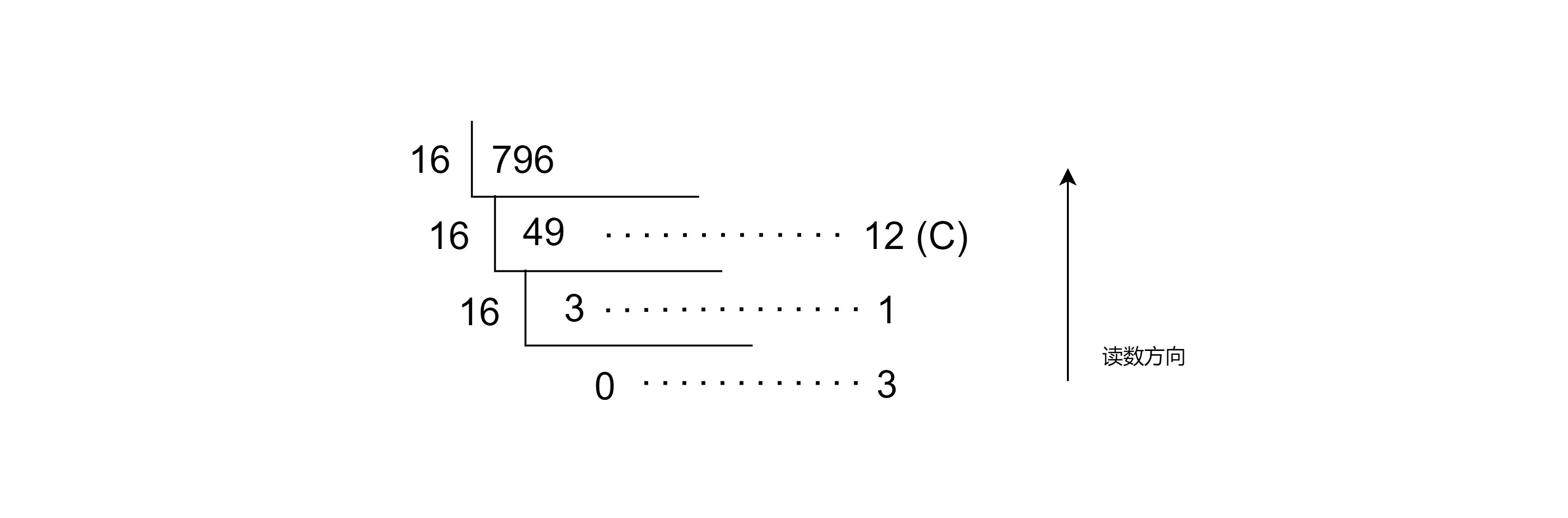
二进制 与 八、十六进制

二进制到八进制

每三位二进制可转化为一位八进制数，如 101B = 5O

不足三位用0补齐

11010111.0100111B = 327.234O

011010111.010011100
3  2  7  .2  3  4

八进制到二进制

原理同上，将八进制每位拆分为三位二进制数，再拼接到一起

二进制到十六进制

每四位二进制数转化为一位十六进制数，如 1010B = 10O

不足四位用0补齐

11010111B = D7H

11010111
D   7

十六进制到二进制

原理同上，将十六进制每位拆分为四位二进制数，拼接到一起

八进制 与 十六进制

1. 八进制 到 二进制 到 十六进制

2. 十六进制 到 二进制 到 八进制

参考链接：https://www.cnblogs.com/gaizai/p/4233780.html